Answer:
5698 sq. cm is the answer.
Explanation:
Since dog cannot enter the garden therefore and it can wander as maximum as its rope can move which actually makes a circle. therefore it makes 3rd fourth of circle with radius 49 cm and then one fourth part circle with radius 7 cm with another corner ( From the corner 42 foot away from where the leash begins ,the dog has only 49 - 42 = 7 foot of leash left )
So total area covered by dog =
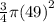 +
+
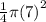
=
![(49)/(4) \pi [49(3) + 1]](https://img.qammunity.org/2019/formulas/mathematics/high-school/qjmfih7gy3x65dokt7w5qmb75ggtkz9r9b.png)
=
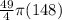
= 37 (49) (
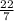
= 37x7x22
=5698 sq cm