Question

Two waves have the same speed. the first has twice the frequency of the second. compare the wavelength of the two waves. 1. the second has one third the wavelength of the first. 2. the first has half the wavelength of the second. 3. the first has one third the wavelength of the second. 4. the second has half the wavelength of the first. 5. they have the s

Answer 1

The basic relationship between frequency, wavelength and speed of a wave is

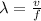
`\lambda= (v)/(f)` (1)
where

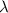
`\lambda` is the wavelength
v is the wave speed
f is the frequency

The problem says the two waves have same speed, so
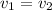
`v_1 = v_2`, and that the first wave has twice the frequency of the second wave, so

`f_1 = 2 f_2`
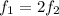
If we use eq,(1), we can compare the two wavelengths

`\lambda_1 = (v_1)/(f_1)= (v_2)/(2f_2)= (1)/(2) (v_2)/(f_2) = (1)/(2) \lambda_2`
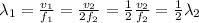
Where in the last step we used
`\lambda_2 = (v_2)/(f_2)`. Therefore, the first wave has half the wavelength of the second wave, so the correct option is option 2).