Question

The height h of the equilateral triangle below is given by y= 5 cot theta where theta = 30 degrees

A) 2.9
B)4.3
C)7.1
D)8.7

Answer 1

To solve this we can take two different approaches:

1. We can substitute theta by 30° and evaluate our expression using a calculator:

`y=5cot( \alpha )`

`y=5cot(30)`

`y=8.7`

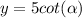
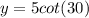
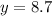2. We can use the unitary circle and the fact that
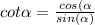
`cot \alpha = (cos( \alpha )/(sin( \alpha ))`, so we can rewrite our expression as follows:

`y=5cot( \alpha )`

`y=5 (cos( \alpha ))/(sin( \alpha ))`

`y= (cos(30))/(sin(30))`
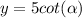
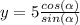
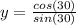
From our unitary circle we can check that
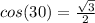
`cos(30)= ( √(3) )/(2)` and
`sin(30)= (1)/(2)`.
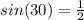
Lets replace those values in our expression and simplify:

`y= ( 5(( √(3) )/(2)))/( (1)/(2) )`

`y=5 √(3)`

`y=8.7`

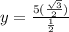
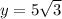
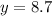
Either way we can conclude that the correct answer is: D)8.7