Question

How do you find the limit?

Answer 1

You can recognize the limit as a derivative. Recall that


`f'(x)=\displaystyle\lim_(h\to0)\frac{f(x+h)-f(x)}h`

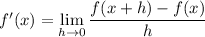
and more to the point,


`f'(1)=\displaystyle\lim_(h\to0)\frac{f(1+h)-f(1)}h`

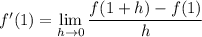
We have


`f(x)=x^4\implies f'(x)=4x^3\implies f'(1)=4`

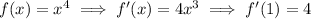
so the answer is B.

We don't actually have to invoke the definition of the derivative. Instead we can just use the definition of
`f(x)`:


`\displaystyle\lim_(h\to0)\frac{(1+h)^4-1^4}h=\lim_(h\to0)\frac{1+4h+6h^2+4h^3+h^4-1}h=\lim_(h\to0)(4+6h+4h^2+h^3)`

which you can see also approaches 4.