Answer:
Option a. [52.78,64.22]
Explanation:
We are given that a random sample of size 18 is drawn from a population that is normally distributed.
Sample mean is 58.5, and the sample standard deviation is found to be 11.5 i.e., X bar = 58.5 and s = 11.5
The pivotal quantity for calculating 95% confidence interval is;
 ~
~
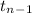
So, 95% confidence interval about population mean is given by;
P(-2.110 <
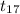 < 2.110) = 0.95
< 2.110) = 0.95
P(-2.110 <
 < 2.110) = 0.95
< 2.110) = 0.95
P(-2.110 *
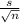 <
<
 < 2.110 *
< 2.110 *
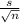 ) = 0.95
) = 0.95
P(X bar - 2.110 *
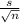 <
<
 < X bar + 2.110 *
< X bar + 2.110 *
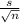 ) = 0.95
) = 0.95
95% confidence interval about
 = [ X bar - 2.110 *
= [ X bar - 2.110 *
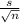 , X bar + 2.110 *
, X bar + 2.110 *
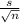 ]
]
= [ 58.5 - 2.110 *
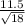 , 58.5 + 2.110 *
, 58.5 + 2.110 *
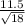 ]
]
= [ 52.78 , 64.22 ]
Therefore, 95% confidence interval about population mean is [52.78 , 64.22].