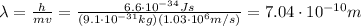Question

(a) an electron has kinetic energy 5.00 ev. find its wavelength.

Answer 1

First, we need to convert electron's kinetic energy into Joules. Keeping in mind that

`1 eV=1.6 \cdot 10^(-19)J`
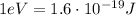
we have

`E=3 eV \cdot 1.6 \cdot 10^(-19) J/eV=4.8 \cdot 10^(-19) J`

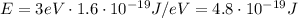
The kinetic energy of the electron is equal to:

`E= (1)/(2)mv^2`
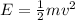
where m is the electron mass and v its speed. If we re-arrange this equation, we can find the electron speed:

`v= \sqrt{ (2E)/(m) }= \sqrt{ (2 \cdot 4.8 \cdot 10^(-19) J)/(9.1 \cdot 10^(-31) kg) } =1.03 \cdot 10^6 m/s`

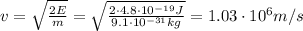
And now we can use De Broglie's relationship to find the electron's wavelength:

`\lambda= (h)/(p)`
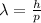
where h is the Planck constant and p=mv is the electron momentum. Substituting numbers, we get

`\lambda= (h)/(mv)= (6.6 \cdot 10^(-34) Js)/((9.1 \cdot 10^(-31)kg)(1.03 \cdot 10^6 m/s))=7.04 \cdot 10^(-10) m`