Question

What is the simplified form of the expression? a1 = -2 a2 = 8 a3= -32

Answer 1

`\bf \stackrel{a_1}{-2}\qquad \qquad \stackrel{a_2}{8}\qquad \qquad \stackrel{a_3}{-32}`

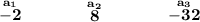
so, notice, from the first term it jumps to 8, then to -32.... hmmm so, we can pretty much see that is being multiplied by "something", meaning is a geometric sequence.

a way to get that "something" namely, the "common ratio", since it's multiplying to get the next term, well, we can simply divide any of the terms by the one before it and, yes, you guessed it, the quotient is the common ratio.

so 8/-2 will give or -32/8, well, you know what that is.


`\bf n^(th)\textit{ term of a geometric sequence} \\\\ a_n=a_1\cdot r^(n-1)\qquad \begin{cases} n=n^(th)\ term\\ a_1=\textit{first term's value}\\ r=\textit{common ratio}\\ ----------\\ a_1=-2\\ r=-4 \end{cases} \implies a_n=-2(-4)^(n-1)`