Question

5^2•3^-1•5^-3/3^4•5^-1•3^-3

Answer 1

Assuming you want the expression to be simplified.

We begin with the following:


`5^(2) * 3^(-1) * (5^-3)/(3^(4)) * 5^(-1) * 3^(-3)`

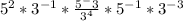
Simplify the first part,
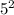
`5^(2)`. That is 25. Now we have this:


`25*3^(-1.5) * (-3)/(3^(4)) * 5^(-1) * 3^(-3)`

Next, simplify
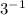
`3^(-1)`, which is 1/3, and get this:


`25* 1/3 * (-3)/(3^(4)) * 5^(-1) * 3^(-3)`

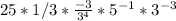
The next part is
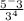
`(5^-3)/(3^(4))`. Simplify the denominator,
`3^(4)`, which is 81. Simplify the numerator, which is 1/125. Then divide 1/125 by 81, which we will keep as a fraction for simplicity's sake, but simplify it to
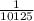
`(1)/(10125)`. Now we have:


`25* 1/3 * (1)/(10125) * 5^(-1) * 3^(-3)`

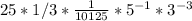
Now simplify
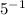
`5^(-1)`, which is 0.2, or 1/5. Now we have:


`25* 1/3 * (1)/(10125) * 0.2 * 3^(-3)`

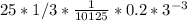
Finally, simplify
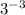
`3^(-3)`. That is 1/27. We have:


`25* 1/3 * (1)/(10125) * 0.2 * 1/27`

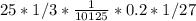
Lastly, multiply them all together! Now we are done, with the product of:


`(1)/(6075)`

That certainly did take a while to type in all the LaTex, so I really hope that helped!

Note- if anything isn't working with the LaTex, just tell me and I'll fix it! (: