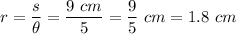Question

May someone please explain how to fill out the table ?

Answer 1

You have the formula written above the table.


`\theta = (s)/(r)`

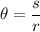
where

`\theta = measure ~of ~central ~angle ~in ~radians`
s = arc length
r = radius

The third lines of both tables need the angle. Since the formula is already solved for theta, the central angle, just plug in s and r and calculate theta.

Left table, third line


`\theta = (s)/(r) = (8 ~in.)/(6~in.) = (4)/(3)`

Right table, third line


`\theta = (s)/(r) = (5~in.)/(8~in.) = (5)/(8)`

For the first line of both tables, you are looking for the arc length. Solve the formula for s, arc length.


`\theta = (s)/(r)`


`s = \theta r`

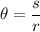
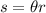
Left table, first line

You have the radius, r = 8 in., and theta, but theta is in degrees. We need theta in radians.


`\theta = 270^\circ * (\pi ~rad)/(180^\circ)`


`\theta = (3 \pi)/(2) ~ rad`


`s = \theta r = (3 \pi)/(2) * 8 in. = 12 \pi ~in.`
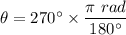
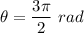
(You're correct.)

Right table, first line


`s = \theta r = (2 \pi)/(3) * 3 ~cm = 2 \pi ~cm`

For the second line of both tables, you are solving for the radius. We now solve the formula for r.


`\theta = (s)/(r)`


`r \theta = s`


`r = (s)/(\theta)`

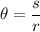
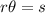
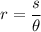
Left table, second line


`r = (s)/(\theta) = (1.5 ~cm)/(1.05) = (10)/(7) ~cm`

Right table, second line


`r = (s)/(\theta) = (9 ~cm)/(5) = (9)/(5) ~cm = 1.8 ~cm`