The surface area of two spheres are in a ratio of 1:16. What is the ratio of their volume?

Question

asked Jun 3, 2019 17.6k views

2 Answers

Dave Sottimano · Answer 1 · 2019-06-09T04:51:44+0000

Let the radius of the 1st sphere be denoted by
r_1

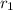
Let the radius of the 2nd sphere be denoted by
r_2

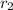
We know that the surface area of any sphere with radius,r is given by the formula:
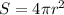$S=4\pi r^2$ where S is the surface area.

Now, let the surface area of the 1st sphere be represented by
S_1 . Therefore,
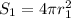
$S_1=4\pi r_1^2$

Likewise, for the second sphere we will have:
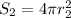
$S_2=4\pi r_2^2$

Now, we have been given that:
(S_1)/(S_2)=(1)/(16)

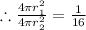
$\therefore (4\pi r_1^2)/(4\pi r_2^2)=(1)/(16)$

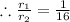
$\therefore (r_1)/(r_2)=\frac {1}{16}$

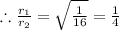
$\therefore (r_1)/(r_2)=\sqrt{(1)/(16)}=(1)/(4)$

Now, we know that the Volume, V of any sphere of radius,r is given by the formula:
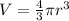
$V=(4)/(3)\pi r^3$

Thus, the ratio of the volumes of the 1st and the 2nd spheres will be given by:

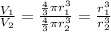$(V_1)/(V_2)=((4)/(3)\pi r_1^3)/((4)/(3)\pi r_2^3) =(r_1^3)/(r_2^3)$ (where symbols have their usual meanings)

Therefore,
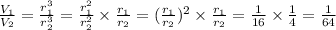
(V_1)/(V_2)=(r_1^3)/(r_2^3)=(r_1^2)/(r_2^2)* (r_1)/(r_2)=((r_1)/(r_2))^2* (r_1)/(r_2)=(1)/(16)* (1)/(4)=(1)/(64)

Thus, the ratio of their volumes is
(1)/(64)