Question

Which statement is true about the graphs of exponential functions?

A. The graphs of exponential functions never exceed the graphs of linear and quadratic functions.
B. The graphs of exponential functions always exceed the graphs of linear and quadratic functions.
C. The graphs of exponential functions eventually exceed the graphs of linear and quadratic functions.
D. The graphs of exponential functions eventually exceed the graphs of linear functions, but not quadratic functions.

Answer 1

c. is the answer i got but im not sure if its correct

Answer 2

Answer: Option 'c' is correct.

Explanation:

Exponential function is in the form of
`f(x)=ab^x`

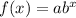
Linear function is in the form of
`f(x)=mx+b`

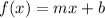
Quadratic function is in the form of
`f(x)=ax^2+bx+c`

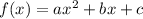
We know that the rate of growth in exponential function is first higher than it goes down whereas the rate of growth is constant in both the linear and quadratic functions.

Hence, The graphs of exponential functions eventually exceed the graphs of linear and quadratic functions.

Thus, Option 'c' is correct.