Answer:
Area of Pizza 1 = 50.24 sq. inch, Area of Pizza 2 = 78.5 sq. inch, Area of Pizza 3 = = 113.04 sq. inch
Thus, the pizza with diameter 8 inch is better to buy.
Explanation:
We are given three pizzas with three different diameters.
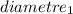 = 8 inch ⇒
= 8 inch ⇒
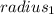 = 4 inch
= 4 inch
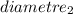 = 10 inch ⇒
= 10 inch ⇒
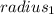 = 5 inch
= 5 inch
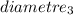 = 12 inch ⇒
= 12 inch ⇒
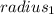 = 6 inch
= 6 inch
Area of Circle = πr², where r is the radius of circle.
Area of Pizza 1 = 3.14 × 4 × 4 = 50.24 sq. inch
Area of Pizza 2 = 3.14 × 5 × 5 = 78.5 sq. inch
Area of Pizza 3 = 3.14 × 6 × 6 = 113.04 sq. inch
We are also given cost for each pizza.
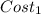 = $9
= $9
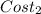 = $12
= $12
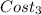 = $18
= $18
To choose which one is a better pizza to buy, we calculate cost per square inch.
Cost per sq. inch =
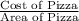
Pizza 1 =
 = 0.18$ per sq. inch
= 0.18$ per sq. inch
Pizza 2 =
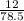 = 0.15$ per sq. inch
= 0.15$ per sq. inch
Pizza 1 =
 = 0.16$ per sq. inch
= 0.16$ per sq. inch
Thus, the pizza with diameter 10 inch is better to buy.