Question

The ratio of the areas of two parallelograms is 4:9. The perimeter of the smaller parallelogram is 20 units. What is the perimeter of the larger parallelogram?

Answer 1

With a ratio, you should think of it in terms of a pie of sorts. In this example, the pie has 13 pieces, 9 of which consist of the perimeter of the large parallelogram and 4 of which consist of the perimeter of the smaller parallelogram. If we know that those 4 pieces of pie and equal to 20 units, then we would divide 20 by 4 to find the value of a single piece. 20/4=5 so a single piece of pie has a value of 5 units. We would then multiply 9 by 5 to find the value equivalent of the 9 pieces of pie. 9(5)=45. Therefore, the perimeter of the larger parallelogram is 45.

Answer 2

30 units

Explanation:

We are given that The ratio of the areas of two parallelograms is 4:9.

So, ratio of sides of parallelograms :
`\sqrt{(4)/(9)} = (2)/(3)`

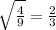
So, sides ratios is 2:3

We are given that The perimeter of the smaller parallelogram is 20 units.

Let the perimeter of the bigger parallelogram be x

So,
`(2)/(3)=(20)/(x)`

`x=(3)/(2) * 20`

`x=30`

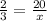
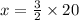
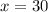
Thus the perimeter of the larger parallelogram is 30 units