Question

The numerator and the denominator of a certain fraction are consecutive odd numbers. If nine is subtracted from the numerator, the ratio of the numerator to the denominator of the new fraction is two to three. What is the original fraction?

1.) 21/33
2.) 31/33
3.) 30/32

Answer 1

the 2nd is the answer :)

Answer 2

Answer: The correct option is (2)
`(31)/(33).`

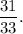
Step-by-step explanation: Given that the numerator and the denominator of a fraction are consecutive odd numbers.

Also, if nine is subtracted from the numerator, the ratio of the numerator to the denominator of the new fraction is two to three.

we are to find the fraction.

Let
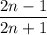`(2n-1)/(2n+1)` be the given fraction, where n is an integer.

Then, according to the given information, we have

`((2n-1)-9)/(2n+1)=(2)/(3)\\\\\\\Rightarrow (2n-10)/(2n+1)=(2)/(3)\\\\\\\Rightarrow 3(2n-10)=2(2n+1)\\\\\Rightarrow 6n-30=4n+2\\\\\Rightarrow 6n-4n=2+30\\\\\Rightarrow 2n=32\\\\\Rightarrow n=(32)/(2)\\\\\Rightarrow n=16.`

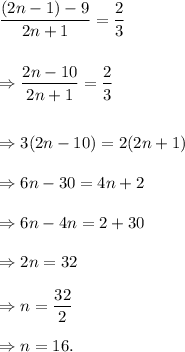
Therefore, the required fraction will be

`(2n-1)/(2n+1)=(2* 16-1)/(2*16+1)=(31)/(33).`

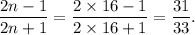
Thus, the fraction is
`(31)/(33).`

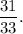
Option (2) is CORRECT.