Answer:
Explanation:
It is given that A spotlight on the ground shines a beam of light to the top of a tree that is 12 m tall. The beam of light makes an angle of 40° with the ground., therefore from the figure drawn, we have
AB=12 m and ∠C=40°.
Using the trigonometry in ΔABC, we have
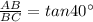
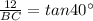

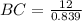
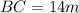
Thus, the distance from the spotlight to the base of the tree is BC=14 m.