Question

The vertices of ΔRST are R(–1,–1), S(–1,11) and T(4,11). Which could be the side lengths of a triangle that is similar but not congruent to ΔRST? 10, 12, and 13 units 5, 24, and 26 units 10, 24, and 26 units 5, 12, and 13 units

Answer 1

10, 24, and 26 units

Explanation:

I got it right on the test

Answer 2

The side lengths could be 10, 24 and 26 units.

We must first find the side lengths. We use the distance formula to do this.

For RT:

`d=√((11--1)^2+(-1--1)^2) \\=√((11+1)^2+(-1+1)^2) \\=√(12^2+0^2)=√(144)=12`

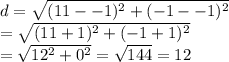
For ST:

`d=√((11-11)^2+(4--1)^2) \\=√(0^2+(4+1)^2)=√(5^2)=√(25)=5`

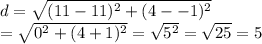
For TR:

`d=√((11--1)^2+(4--1)^2) \\=√((11+1)^2+(4+1)^2)=√(12^2+5^2)=√(144+25)=√(169)=13`

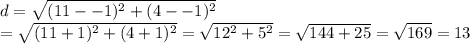
Our side lengths, from least to greatest, are 5, 12 and 13.

To be similar but not congruent, the side lengths must have the same ratio between corresponding sides but not be the same length. 10, 24 and 26 are all 2x the original side lengths, so this works.