Question

Given that x + y = 13 and xy = 24, find the distance from the point (x, y) to the origin.

Answer 1

Answer: Distance from the point (x, y) to the origin is approximately 11 units.

Step-by-step explanation: Given equations x+y=13 and xy =24.

Solving first equation for y, we get

y = 13-x.

Substituting y=13-x in second equation, we get

x(13-x)= 24.

13x -x^2=24.

-x^2+13x =24.

-x^2+13x -24=0.

Dividing each term by -1, we get

x^2-13x+24=0.

Applying quadratic formula

`x=(-b\pm √(b^2-4ac))/(2a)`

`\mathrm{For\:}\quad a=1,\:b=-13,\:c=24:\quad x=(-\left(-13\right)\pm √(\left(-13\right)^2-4\cdot \:1\cdot \:24))/(2\cdot \:1)`

`x=(-\left(-13\right)+√(\left(-13\right)^2-4\cdot \:1\cdot \:24))/(2\cdot \:1):\quad (13+√(73))/(2) =10.77`

`x=(-\left(-13\right)-√(\left(-13\right)^2-4\cdot \:1\cdot \:24))/(2\cdot \:1):\quad (13-√(73))/(2)=2.23`

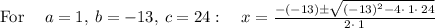
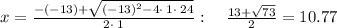
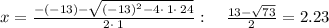
Plugging x=10.77 in first equation

y= 13-10.77 = 2.23

and plugging x=2.23 in first equation, we get

y = 13-2.23 = 10.77.

Therefore, (x,y) are (10.77, 2.23) and (2.23, 10.77).

Now, we need to find the distance of (x,y) from origin (0,0).

Applying distance formula :

`\mathrm{Compute\:the\:distance\:between\:}\left(x_1,\:y_1\right),\:\left(x_2,\:y_2\right):\quad √(\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2)`

`=√(\left(10.77-0\right)^2+\left(2.23-0\right)^2)`

`=10.9984\`

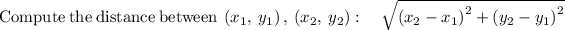
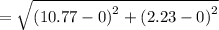
≈ 11 units.

Therefore, distance from the point (x, y) to the origin is approximately 11 units.