Question

Solve the logarithmic equation. When necessary, round answer to the nearest hundredth. logx 36 = 2

Answer 1

`x=6`

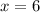
Explanation:

We have been given a logarithmic equation
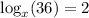`\text{log}_x(36)=2`. We are asked to solve our given equation.

Using log rule
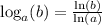`\text{log}_a(b)=\frac{\text{ln}(b)}{\text{ln}(a)}`, we will get:

`\text{log}_x(36)=\frac{\text{ln}(36)}{\text{ln}(x)}`

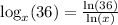
Substituting back this value, we will get:

`\frac{\text{ln}(36)}{\text{ln}(x)}=2`

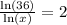
Multiply both sides by
`\text{ln}(x)`:

`\frac{\text{ln}(36)}{\text{ln}(x)}*\text{ln}(x)=2*\text{ln}(x)`

`\text{ln}(36)=2*\text{ln}(x)`

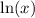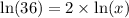
Switch sides:

`2*\text{ln}(x)=\text{ln}(36)`

`2*\text{ln}(x)=\text{ln}(6^2)`

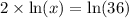
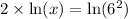
Using property
`\text{log}_a(x^b)=b\cdot \text{log}_a(x)`, we will get:

`2*\text{ln}(x)=2\cdot \text{ln}(6)`

`\frac{2*\text{ln}(x)}{2}=\frac{2\cdot \text{ln}(6)}{2}`

`\text{ln}(x)=\text{ln}(6)`

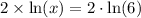
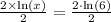
Since base of both sides are equal, therefore, the value of x is 6.