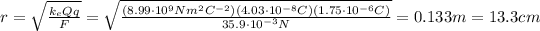Question

A sphere of radius 5.15 cm and uniform surface charge density +12.1 µC/m2 exerts an electrostatic force of magnitude 35.9 ✕ 10-3 N on a point charge +1.75 µC. Find the separation between the point charge and the center of the sphere.

Answer 1

The radius of the sphere is r=5.15 cm=0.0515 m, and its surface is given by

`A=4 \pi r^2 = 4 \pi (0.0515 m)^2 = 0.033 m^2`

So the total charge on the surface of the sphere is, using the charge density

`\rho=+1.21 \mu C/m^2 = +1.21 \cdot 10^(-6) C/m^2`:

`Q= \rho A = (+1.21 \cdot 10^(-6) C/m^2)(0.033 m^2)=4.03 \cdot 10^(-8)C`

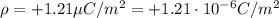
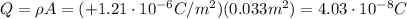
The electrostatic force between the sphere and the point charge is:

`F=k_e (Qq)/(r^2)`
where
ke is the Coulomb's constant
Q is the charge on the sphere

`q=+1.75 \muC = +1.75 \cdot 10^(-6)C` is the point charge
r is their separation

Re-arranging the equation, we can find the separation between the sphere and the point charge:

`r=\sqrt{ (k_e Q q)/(F) }= \sqrt{ ((8.99 \cdot 10^9 Nm^2 C^(-2))(4.03 \cdot 10^(-8) C)(1.75 \cdot 10^(-6)C))/(35.9 \cdot 10^(-3)N) }=0.133 m=13.3 cm`