Question

Given: a and b are parallel and c is a transversal. Prove: ∠2 ≅ ∠7 Use the drop-down menus to complete the paragraph proof showing that alternate interior angles are congruent. We know that lines a and b are parallel and that line c is a transversal because that is given. We can tell that angles 2 and 5 are congruent because angles are congruent. Angles 5 and 7 are congruent because angles by parallel lines cut by a transversal are congruent. Therefore, angles 2 and 7 are congruent based on the .

Answer 1

its Vertical, Corresponding and Transitive property

Answer 2

Transitive property of congruence angles.

Explanation:

Given a and b are parallel lines and c is a transversal .

To prove that
`\angle 2\cong \angle 7`

Proof:

Line
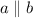`a\parallel b` and c is a transversal line because we are given this. We can say that angles 2 and 5 are congruent by vertical opposite angle theorem because these angles are vertical opposite angles .Vertical opposite angles are those angles which are made by two intersecting lines and opposite to each other. We can say that angles 5 and 7 are congruent by corresponding angles theorem .Because angle 5 and 7 are corresponding angles .Corresponding angle are those angle which are made on the same side at each intersection where a transversal line crosses two other lines.

Therefore, by transitive property of congruence angles angle 2 and angle 7 are congruent.

Hence,
`\angle 2\cong \angle 7`.