Question

Sam and Fred are debating their current investment strategy. Sam’s money is invested at 9% compound interest. Fred’s money is invested at 9% simple interest.

Whose money will double faster? Calculate the amount of time it will take for the money to double in each scenario. Use these calculations to support your response. Show all work.

Answer 1

Sam's money will double faster.

The formula for compound interest is
A=p(1+r)ˣ, where A is the total amount in the account, p is the principal you invest, r is the interest rate as a decimal, and x is the amount of time.

If we want to represent the money being doubled, we would use 2p for A:
2p=p(1+0.09)ˣ
2p=p(1.09)ˣ

Divide both sides by p:
2p/p = p(1.09)ˣ/p
2 = 1.09ˣ

Using logarithms to solve this,

`\log_(1.09)2=x \\ \\8.04=x`

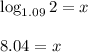
The formula for simple interest is
I = prt

If we want to find the amount of time to double the principal, this means the amount of interest would be equal to the principal invested:
p = p(0.09)t

Dividing both sides by p,
p/p = p(0.09)t/p
1 = 0.09t

Dividing both sides by 0.09,
1/0.09 = t
11.11 = t