Question

Suppose that circles A and B have a central angle measuring 100°. Additionally, the measure of the sector for circle A is 10π m2 and for circle B is 40π m2.If the radius of circle A is 6 m, what is the radius of circle B?

A) 8 m
B) 10 m
C) 12 m
D) 16 m

Answer 1

12 m

10π40π = 62x2
x = 12

When circles have the same central angle measure, the ratio of measure of the sectors is the same as the ratio of the radii squared.

Answer 2

OptionC

Explanation:

A circle A has radius 6m.

One sector has area as 10 pi m^2

central angle = 100 degrees

Area of the sector =
`(100)/(360) \pi(6)^2`

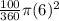
Area of sector in circle B =
`(100)/(360) \pi(r)^2`

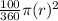
where r=radius of circle B

Hence ratio of these would be the ratio of square of radii

i.e.
`(10)/(40) =((6)/(r) )^2\\(1)/(2) =(6)/(r) \\r=12 m`

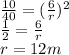
So radius of circle B = 12m

Option C is right