Question

On which of the following intervals is the function f(x) = 4 cos(2x − π) decreasing?

x = pi over 2 to x = π
x = 0 to x = pi over 2
x = pi over 2 to x = 3 pi over 2
x = π to x = 3 pi over 2

Answer 1

The answer is x= π/2 to x= π
(just did this question & got it right)

Answer 2

Answer: Option (A) is correct.

Step-by-step explanation: The given function is

`f(x)=4\cos (2x-\pi).`

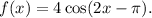
We are to select the interval in which the above function is decreasing.

For the interval
`x=(\pi)/(2)~\textup{to}~x=\pi,`

`f((\pi)/(2))=4\cos(2* (\pi)/(2)-\pi)}=4\cos(\pi-\pi)=4\cos 0=4(1)=4,\\\\f(\pi)=4\cos(2\pi-\pi)=4\cos \pi=4(-1)=-4.`

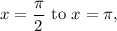
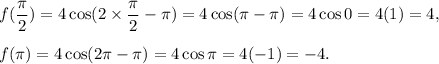
So, f(x) is decreasing in this interval.

For the interval
`x=0~\textup{to}~x=(\pi)/(2)`,

`f(0)=4\cos(2* 0-\pi)}=4\cos(0-\pi)=4\cos pi=4(-1)=-4,\\\\f((\pi)/(2))=4\cos(2* (\pi)/(2)-\pi)=4\cos (\pi-\pi)=4(1)=4.`

So, f(x) isnot decreasing in this interval.

For the interval
`x=(\pi)/(2)~\textup{to}~x=(3\pi)/(2),`

`f((\pi)/(2))=4\cos(2* (\pi)/(2)-\pi)}=4\cos(\pi-\pi)=4\cos 0=4(1)=4,\\\\f((3\pi)/(2))=4\cos(2* (3\pi)/(2)-\pi)=4\cos (3\pi-\pi)=4\cos 2\pi=4(1)=4.`

So, f(x) is not decreasing in this interval.

For the interval
`x=\pi~\textup{to}~x=(3\pi)/(2),`

`f((\pi)/(2))=4\cos(2* (\pi)/(2)-\pi)=4\cos (\pi-\pi)=4(1)=4,\\\\f((3\pi)/(2))=4\cos(2* (3\pi)/(2)-\pi)=4\cos (3\pi-\pi)=4\cos 2\pi=4(1)=4.`

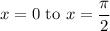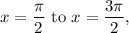
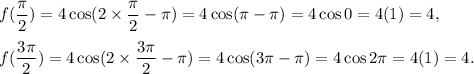
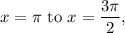
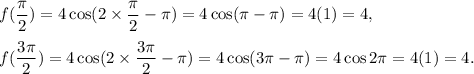
So, f(x) is not decreasing.

Thus, (A) is the correct option.