Here barrel of tomato sauce has spilled on a tile floor.
The function
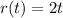 represents how the sauce is flowing, where, 't' represents time in minutes, and 'r' represents how far the sauce is spreading.
represents how the sauce is flowing, where, 't' represents time in minutes, and 'r' represents how far the sauce is spreading.
The spilled sauce is creating a circular pattern on the tile and the area of pattern is expressed as

A. Now we have to find the area of circle of spilled sauce as a function of time:
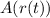 .
.
Now, we know that
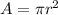
and
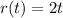
plugging the value of 'r' as function of time in the area of the pattern, we get:

So the area of the circular pattern as a function of time is given as:
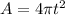
B. We have to find how large is the area of spilled sauce after 5 minutes.
plugging the value of 't' in the equation of the area as a function of time,

we get:
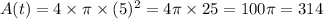
(we have taken
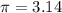 )
)
Therefore,
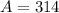 square units
square units