Question

Can someone please explain how to solve this problem fast! thanks

Answer 1

`\sf 6b^2-5b=4`

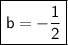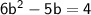
Subtract 4 to both sides:


`\sf 6b^2-5b-4=0`

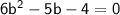
Factor:

We want to find out what two numbers will multiply to get
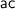
`\sf ac` and add up to get
`\sf b`. Our quadratic is in the form of
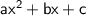
`\sf ax^2+bx+c`. So in this case, a is 6, b is -5, and c is -4.
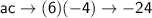
`\sf ac\rightarrow (6)(-4)\rightarrow -24`. And we know that b is -5, so we want to find two numbers that will multiply to get -24 and add up to get -5. These two numbers are 3 and -8. Rewrite -5b in the quadratic with these:


`\sf 6b^2+3b-8b-4=0`

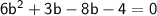
Now factor them separately:


`\sf (6b^2+3b)+(-8b-4)=0\rightarrow 3b(2b+1)-4(2b+1)=0`

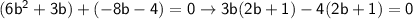
As you can see (2b + 1) is common for both terms, so we can just group the beginning of the terms together to get:


`\sf (3b-4)(2b+1)=0`

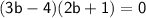
Set each one equal to 0 and solve for 'b':


`\sf 3b-4=0`

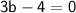
Add 4 to both sides:


`\sf 3b=4`

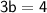
Divide 3 to both sides:


`\boxed{\sf b=(4)/(3)}`


`\sf 2b+1=0`

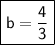
Subtract 1 to both sides:


`\sf 2b=-1`

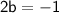
Divide 2 to both sides:


`\boxed{\sf b=-(1)/(2)}`