Question

The coordinates of a quadrilateral are (1,3), (7,-3), (1,-9), and (-5,-3). Which shape is formed select all that apply

-kite
-rectangle
-rhombus
-square
-trapezoid

Answer 1

Answer: rectangle , rhombus , and square

Explanation:

i got it right :)

Answer 2

rectangle , rhombus , and square

Explanation:

First we find the slope of the line between each pair of points. We will first name each point:

A(1, 3); B(7, -3); C(1, -9); and D(-5, -3).

The formula for slope is

`m=(y_2-y_1)/(x_2-x_1)`

This means the slope for AB is

m = (3--3)/(1-7) = (3+3)/(-6) = 6/-6 = -1

The slope for BC is

m = (-3--9)/(7-1) = (-3+9)/6 = 6/6 = 1

The slope for CD is

m = (-9--3)/(1--5) = (-9+3)/(1+5) = (-6)/6 = -1

The slope for DA is

m = (-3-3)/(-5-1) = (-6)/(-6) = 1

If two sides are parallel, then the slopes of their lines are the same. The slopes of AB and CD are the same; this means they are parallel. The slopes of BC and DA are the same; this means they are parallel. This makes this figure a parallelogram.

If two sides form a right angle, then their slopes are negative reciprocals. The slopes of AB and BC are negative reciprocals, so they form a right angle. The slopes of BC and CD are negative reciprocals, so they form a right angle. The slopes of CD and AB are negative reciprocals, so they form a right angle. This means the fourth angle must be a right angle as well. This makes the figure a rectangle.

We next use the distance formula to find the length of each side:

`d = √((y_2-y_1)^2+(x_2-x_1)^2)`

The length of AB is

`d=√((3--3)^2+(1-7)^2)=√(6^2+(-6)^2)=√(36+36)=√(72)`

The length of BC is

`d=√((-3--9)^2+(7-1)^2)=√(6^2+6^2)=√(36+36)=√(72)`

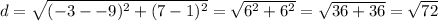
The length of CD is

`d=√((-9--3)^2+(1--5)^2)=√((-6)^2+6^2)=√(36+36)=√(72)`

The length of DA is

`d=√((-3-3)^2+(-5-1)^2)=√((-6)^2+(-6)^2)=√(36+36)=√(72)`

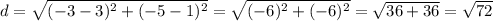
Since all four sides have the same length, the figure is a square.