Question

Which statement is true about the graphs of the two lines y=-8x - 5/4 and y= 1/8x + 4/5? The lines are perpendicular to each other because –8 and are opposite reciprocals of each other. The lines are perpendicular to each other because and are opposite reciprocals of each other. The lines are neither parallel nor perpendicular to each other because –8 and are not opposite reciprocals of each other. The lines are neither parallel nor perpendicular to each other because and are not opposite reciprocals of each other.

Answer 1

1. The lines are perpendicular to each other because -8 and 1/8 are negative reciprocals of each other.

Step-by-step explanation:

We have been given equations of two lines as:
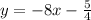`y=-8x-(5)/(4)` and
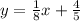`y=(1)/(8)x+(4)/(5)`. We are asked to choose the correct statement about our given lines.

We can see both equations of our given lines in slope-intercept form of equation:
`y=mx+b`, where, m represents slope of line and b represents y-intercept.

We can see that the slopes of our lines are -8 and 1/8.

Since we know that the slopes of perpendicular lines are negative reciprocal of each other and -8 and 1/8 are negative reciprocal of each other.

Two numbers are negative reciprocal if their product is -1.

`-8* (1)/(8)=-1`

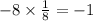
Therefore, our given lines are perpendicular lines and 1st statement is the correct choice.

Answer 2

Hi there!

The lines given in the problem are perpendicular to each other because they are opposite reciprocals. An opposite reciprocal is when the original slope (-8) is made opposite, which is negative or positive depending on the number (8) and is flipped upside down, or the numerator becomes the denominator and vice-versa (1/8). Opposite reciprocals are also shown by when the two slopes are multiplied together, it is equal to -1, showing that the lines are perpendicular. (-8/1 x 1/8 = -1)

Hope this helps!! :)