Question

Both circle A and circle B have a central angle measuring 50°. The area of circle A's sector is 36π cm2, and the area of circle R's sector is 64π cm2. Which is the ratio of the radius of circle Q to the radius of circle R?

Answer 1

7/8π

The circles have the same central angle measures; therefore, the ratio of the intercepted arcs is the same as the ratio of the radii.

23 = 34πx
x = 98π

Answer 2

The ratio of the radius of circle A to the radius of circle B are 3:4.

Step-by-step explanation:

Area of a circle is

`Area =(\theta)/(360)\pi r^2`

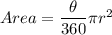
Let radius of circle A and circle B are r₁ and r₂ receptively.

Both circle A and circle B have a central angle measuring 50°.

Area of A's sector is

`Area =(50)/(360)\pi r_1^2`

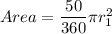
Area of B's sector is

`Area =(50)/(360)\pi r_2^2`

The area of circle A's sector is 36π cm2, and the area of circle R's sector is 64π cm2. So, the ratio of area is

`((50)/(360)\pi r_1^2)/((50)/(360)\pi r_2^2)=(36\pi)/(64\pi)`

Cancel out the common factors.

`(r_1^2)/(r_2^2)=(9)/(16)`

`((r_1)/(r_2))^2=(9)/(16)`

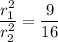
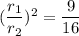
Taking square root on both sides.

`(r_1)/(r_2)=(3)/(4)`

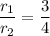
Therefore, the ratio of the radius of circle A to the radius of circle B are 3:4.