Question

Click an item in the list or group of pictures at the bottom of the problem and, holding the button down, drag it into the correct position in the answer box. Release your mouse button when the item is place. If you change your mind, drag the item to the trashcan. Click the trashcan to clear all your answers.

Complete the following proof.

Prove: The opposite sides of a parallelogram are equal.

Answer 1

Explanation:

Prove: The opposite sides of parallelogram are equal.

Proof: The given points are A(0,0) and D(c,d) are:

Using distance formula, we have

`AD=√((c-0)^2+(d-0)^2)=√(c^2+d^2)`

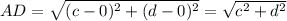
The given points are B(b,0) and C(b+c,d) are:

Using distance formula, we have

`BC=√((b+c-b)^2+(d-0)^2)=√(c^2+d^2)`

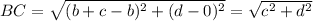
The given points are A(0,0) and B(b,0) are:

Using distance formula, we have

`AB=√((b-0)^2+(0-0)^2)=√(b^2+0^2)=√(b^2)`

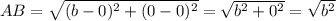
The given points are C(b+c,d) and D(c,d) are:

Using distance formula, we have

`CD=√((c-(b+c))^2+(d-d)^2)=√(b^2+0^2)=√(b^2)`

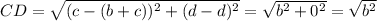
Hence, AD=BC and AB=CD, therefore opposite sides of parallelogram are equal.

Answer 2

The first thing we should do is find AD:
AD=root((c-0)^2 + (d-0)^2)=root((c)^2 + (d)^2)
We now look for the value of BC:
BC=root(((b+c) - b)^2+(d-0)^2)=root((c)^2+(d)^2)
Then, we look for AB:
AB=root((b-0)^2 + (0-0)^2)=root((b)^2 + (0)^2)=root((b)^2)
Finally, we look for the value of CD: CD=root((c-(b+c))^2 + (d-d)^2)
CD=root((b)^2 + (0)^2)
CD=root((b)^2)