Question

An electron is released above the earth's surface. a second electron directly below it exerts just enough of an electric force on the first electron to cancel the gravitational force on it. find the distance between the two electrons.

Answer 1

The gravitational force on the first electron is equal to its weight:

`F=m_e g`
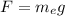
where
`m_e = 9.1 \cdot 10^(-31) kg` is the electron mass and
`g=9.81 m/s^2` is the gravitational acceleration. Substituting, we find that the gravitational force is

`F=(9.1 \cdot 10^(-31) kg)(9.81 m/s^2)=8.9 \cdot 10^(-30) N`

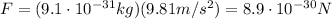
Instead, the electric force exerted by the second electron on the first one is

`F=k_e (q_1 q_2)/(r^2)`
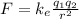
where

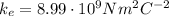
`k_e = 8.99 \cdot 10^9 N m^2 C^(-2)` is the Coulomb's constant

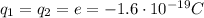
`q_1 = q_2 = e = -1.6 \cdot 10^(-19) C` is the charge of each electron
r is the distance between them.

The problem says that the distance r is such that the electric force cancels the gravitational force, so the electric force must be equal to the gravitational force:
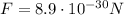
`F=8.9 \cdot 10^(-30) N`. So, if we use this value in the formula of the electric force, we can calculate the distance r between the two electrons:

`r=\sqrt{k_e (q_1 q_2)/(F) }=\sqrt{(8.99 \cdot 10^9) ((-1.6 \cdot 10^(-19) C)^2)/(8.9 \cdot 10^(-30)N) }=5.1 m`