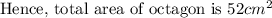Question

The following octagon is formed by removing four congruent right triangles from a rectangle. What is the total area of the octagon

Answer 1

`\text{Total area of octagon is }52 cm^2`

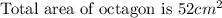
Explanation:

we have to find total area of octagon formed by removing four congruent right triangles from a rectangle.

First we have to find the the area of rectangle whose length and breadth are

Length=2+6+2=10 cm

Breadth=2+2+2=6 cm

`Area=Length* breadth=10* 6=60 cm^2`

Area of 4 congruent right triangles are

`=4((1)/(2)* 2* 2)=4* 2=8 cm^2`

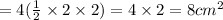
Area of octagon=area of rectangle-area of 4 triangles

=60-8=52 cm^2[/tex]

`\text{Hence, total area of octagon is }52 cm^2`

Answer 2

To find the total area of the octagon you can find the area of the rectangle that is created by the entire figure and subtract the areas of the four congruent right triangles.

(10 cm x 6 cm) - [4(1/2 x 2 x 2)]
60 cm² -8 cm² = 52 cm²

The total area of the octagon is 52 cm².