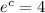Question

Which exponential equation is equivalent to the logarithmic equation below?

c = ln 4

Answer 1

recall that ln() is just a shorthand for logₑ or the natual logarithm.


`\bf \textit{exponential form of a logarithm} \\\\ log_a b=y \implies a^y= b\qquad\qquad % exponential notation 2nd form a^y= b\implies log_a b=y \\\\ -------------------------------\\\\ c=ln(4)\implies c=log_e(4)\implies e^c=4`

Answer 2

Hence, the exponential equation equivalent to logarithmic function
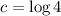`c=\log 4` is:

`e^c=4`

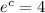
Explanation:

We are given a exponential function as:

`c=\log 4`

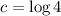
We are asked to find the exponential function which is equivalent to this given logarithmic function.

We know that exponential function and logarithmic function are inverse of each other.

If we are given a logarithmic function as:

`y=\log _ax`

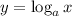
Then it's equivalent exponential function is given as:

`x=a^y`

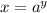
with the condition:

a>0 and a≠1.

Hence, the exponential equation equivalent to logarithmic function
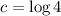`c=\log 4` is:

`e^c=4`