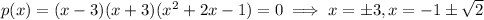Can someone please solve this for me by using synthetic division and write it in steps x ^(4)+2x ^(3)-10 x^(2)-18x+9=0

Question

Can someone please solve this for me by using synthetic division and write it in steps


`x ^(4)+2x ^(3)-10 x^(2)-18x+9=0`

Answer 1

If you don't want to test random numbers to see what reduces the polynomial to 0, you can try applying the rational root theorem to narrow down the possible choices. The RRT says that the polynomial *may* have rational roots determined by the leading and constant coefficients.

Factors of constant term:
`\pm1,\pm3,\pm9`
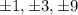
Factors of leading term's coefficient:
`\pm1`
Possible rational roots:
`\pm1,\pm3,\pm9`
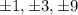
(i.e. divide all factors of constants terms by all factors of leading coefficient)

Denoting the given polynomial by
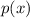
`p(x)`, we get


`p(1)=-16`

`p(-1)=16`

`p(3)=0`

`p(-3)=0`

`p(9)=7056`

`p(-9)=4464`

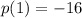
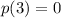
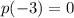
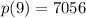
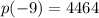
which tells us that
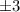
`\pm3` are actually roots to
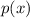
`p(x)`. In other words, we can factor
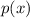
`p(x)` as


`p(x)=(x-3)(x+3)(\text{some quadratic})`

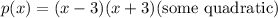
Now that we know some roots to the polynomial, we can factor via synthetic division. First by
`x-3`:

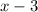
3 | 1 2 -10 -18 9
. | 3 15 15 -9
- - - - - - - - - - - - - - - - - -
. | 1 5 5 -3 0

which says


`(x^4+2x^3-10x^2-18x+9)/(x-3)=x^3+5x^2+5x-3`

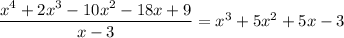
Next by
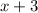
`x+3` (this time dividing the cubic above):

-3 | 1 5 5 -3
. | -3 -6 3
- - - - - - - - - - - - - -
. | 1 2 -1 0

which means


`(x^3+5x^2+5x-3)/(x+3)=x^2+2x-1`

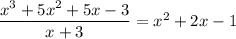
Putting both steps together, we found that


`x^4+2x^3-10x^2-18x+9}{(x-3)(x+3)}=x^2+2x-1`

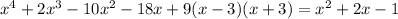
(FYI: There's an alternative algorithm that we could use to immediately divide
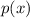
`p(x)` by
`(x-3)(x+3)=x^2-9`)

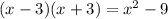
so it turns out that
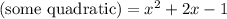
`(\text{some quadratic})=x^2+2x-1`, whose roots you can find with the quadratic formula. We get


`p(x)=(x-3)(x+3)(x^2+2x-1)=0\implies x=\pm3, x=-1\pm\sqrt2`