Question

Quadrilateral ABCD ​ is inscribed in this circle.

What is the measure of angle A?



Enter your answer in the box.

°

Answer 1

The answer should be 88

Hope this helps and have good day

Answer 2

the sum of all interior angles in a polygon is

180(n-2), where n = sides, well, this is a QUADrilateral, so it has 4 sides, so the total is 360°.

now, let's find what angle C is first,


`\bf \stackrel{A}{(2x-40)}+\stackrel{B}{(116)}+C+\stackrel{D}{(x)}=360\implies C+3x+76=360 \\\\\\ C+3x=284\implies C=284-3x`

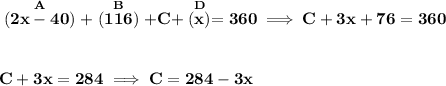
now, recall the "inscribed quadrilateral conjecture", where opposite angles are "supplementary angles", thus


`\bf \stackrel{\measuredangle A}{(2x-40)}+\stackrel{\measuredangle C}{(284-3x)}=180\implies -x+244=180 \\\\\\ 64=x\\\\ -------------------------------\\\\ \measuredangle A=2(64)-40`