Question

A school store must spend no more than $225 for an order of pens and pencils. Each pen costs $0.75, and each pencil costs $0.25. This relationship is shown in the graph. The store needs at least 100 more pencils than pens. Which choice is a reasonable solution?

A.)300 pens and 900 pencils
B.)200 pens and 300 pencils
C.)300 pens and 200 pencils
D.)100 pens and 200 pencils

Answer 1

Answer: Option 'B' is correct.

Explanation:

Since we have given that

Cost of each pen = $0.75

Cost of each pencil = $0.25

Let the number of pen is bought be 'x'.

Let the number of pencil is bought be 'y'.

According to question, our inequality becomes

`0.75x+0.25y\leq \$225-----------(1)\\\\and\\\\y-x\geq 100----------(2)`

If we consider the first option :

A) 300 pens and 900 pencils:

`0.75* 300+0.25* 900\\leq 225\\\\225+225\\leq 225\\\\450\\leq 225`

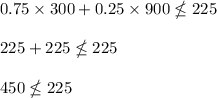
B) 200 pens and 300 pencils

`0.75* 200+0.25* 300\leq 225\\\\150+75=225\\\\225=225`

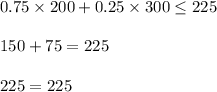
C) 300 pens and 200 pencils

`0.75* 300+0.25* 200\leq 225\\\\225+50\\leq 225\\\\275\\leq 225`

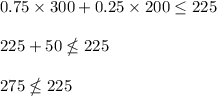
D) 100 pens and 200 pencils

`0.75* 100+0.25* 200\leq 225\\\\75+50\leq 225\\\\125\leq 225`

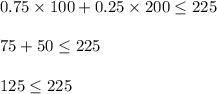
Since options 'B' and 'D' are both correct but as we can see that from option 'B' we get sum of 500 pen and pencils whereas from option 'D' , we get sum of 300 pens and pencils.

So, Option 'B' is correct.

Answer 2

The correct answer is:

B) 200 pens and 300 pencils.

Explanation:

To use the graph, we must determine which variable represents pens and which represents pencils. Since we know there are more pencils than pens, and the region graphed goes higher on the y-axis than it does on the x-axis, we determine that y represents the number of pencils and x represents the number of pens.

Now we check each answer choice using the graph.

For A, 300 pens and 900 pencils, we go to 300 on the x-axis and 900 on the y-axis. This is not in the graphed region, so this is not a reasonable solution.

For B, 200 pens and 300 pencils, we go to 200 on the x-axis and 300 on the y-axis. This is on the border of the region, so this is a reasonable solution.

For C, 300 pens and 200 pencils, we go to 300 on the x-axis and 200 on the y-axis; this is not in the graphed region, so this is not a reasonable solution.

For D, 100 pens and 200 pencils, we go to 100 on the x-axis and 200 on the y-axis; this is within the graphed region, so this is a reasonable solution; however, the store would likely want to purchase as many as possible, so this is not the best solution.