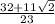Question

Rationalize the denominator of the following expression and simplify:

6+ *radical 2*
___________

5- *radical 2*

Answer 1

The rationalized and simplified expression is:
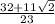`(32+11 √(2) )/(23)` therefore, option b is correct.

To rationalize the denominator of the given expression, we can use the conjugate technique. The conjugate of the denominator
`(5- √(2) ) is (5+ √(2) )`

Now, multiply both the numerator and denominator by the conjugate:

​
`(6 + √(2 ) )/(5 - √(2) ) * (5+ √(2) )/(5+ √(2))`

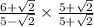
Now, multiply the numerators and denominators separately:

Numerator:

`(6+ √(2) )(5+ √(2) )`

Denominator:

`(5- √(2) )(5+ √(2) )`

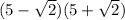
Let's calculate both:

Numerator:

`(6+ √(2) )(5+ √(2) )=30+6 √(2)​ +5 √(2)​ + 2=32+11 √(2)`

​Denominator:

`(5-√(2) )(5+ √(2) )=25-2=23`

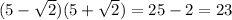
Now, the expression becomes:

`(32+11 √(2) )/(23)`

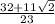
So, the rationalized and simplified expression is:
`(32+11 √(2) )/(23)`

Answer 2

to "rationalize the denominator" is another way to say, getting rid of that pesky radical at the bottom.

we'll simply start by multiplying top and bottom by the "conjugate" of the denominator, recall difference of squares, anyhow, let's do so


`\bf \cfrac{6+√(2)}{5-√(2)}\cdot \cfrac{5+√(2)}{5+√(2)}\implies \cfrac{(6+√(2))(5+√(2))}{(5-√(2))(5+√(2))}\implies \cfrac{(6+√(2))(5+√(2))}{5^2-(√(2))^2} \\\\\\ \cfrac{30+6√(2)+5√(2)+(√(2))^2}{25-2}\implies \cfrac{30+11√(2)+2}{23}\implies \cfrac{32+11√(2)}{23}`