Question

Given the function f(x) =3(x+2)-4, solve for the inverse function when x=2

Answer 1

The inverse function is f(x) =
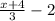`(x + 4)/(3) - 2`, which makes the inverse at x = 2 equal to 0.

All inverse functions can be found by switching the x and f(x) values. Once that is done, solve for the new f(x) value. The result will be the inverse of the original function. The step-by-step process is below.

f(x) = 3(x + 2) - 4 ----> Switch the x and f(x)

x = 3(f(x) + 2) - 4 ----> Add 4 to both sides

x + 4 = 3(f(x) + 2) ----> Divide both sides by 3

`(x + 4)/(3)` = f(x) + 2 ----> Subtract 2 from both sides.

f(x) =
`(x + 4)/(3) - 2`

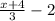
The end is your inverse function. So then we can evaluate when x = 2.

f(x) =
`(x + 4)/(3) - 2`

f(2) =
`(2 + 4)/(3) - 2`

f(2) =
`(6)/(3) - 2`

f(2) =
`2 - 2`

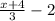
f(2) = 0