To solve the first part we are going to use the formula for the nth therm of geometric sequence:
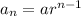
where

is the nth term

is the first term

is the ratio

is the position of the term in the sequence
a. The ratio of a geometric sequence is
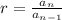
. We know for our problem that
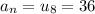
and
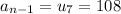
. Lets replace those values in our formula to find

:

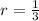
We can conclude that the ratio of our geometric sequence is
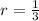
.
b. To find

we are going to use the formula for the nth therm of geometric sequence, the ratio, and the given fact that
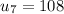
:
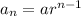
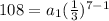
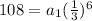
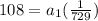
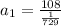
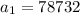
We can conclude that the first therm,

, of our geometric sequence is 78732.
c. To solve this one we are going to use the formula for the sum of the first nth terms of a geometric sequence:
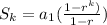
where
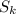
is the sum of the first

terms

is the first term

is the common ratio

is the number of terms
We know for our problem that
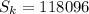
, and we also know for previous calculations that
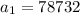
and
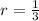
. So lets replace those values in our formula to find

:
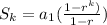
![118096=78732[ (1-( (1)/(3))^k )/(1- (1)/(3) ) ]](https://img.qammunity.org/2019/formulas/mathematics/high-school/vpjdz6rj1hsxq0t1euqi63kgr6lrip91k9.png)
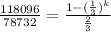
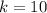
We can conclude the the sum of the first 10 terms of our geometric sequence is 118096.