Question

Evaluate the exponential function ƒ(x) = (1/2)^x

x      -4    -1    0     1      3
ƒ(x) 16    ?    1    1/2   1/8

Which value completes this table?
A.12
B.8
C.4
D.2

Answer 1

D. 2 is correct.

Explanation:

We are given the function,
`f(x)=((1)/(2))^(x)`

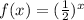
It is required to find the value of f(x) when x = -1.

So, we will substitute the value of x= -1 in the function.

This gives us,

`f(x)=((1)/(2))^(x)`

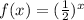
implies
`f(-1)=((1)/(2))^(-1)`

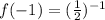
As, we know,

`((1)/(b))^(-1)=(1)/(b^(-1))=b`

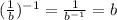
So,
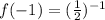`f(-1)=((1)/(2))^(-1)` implies
`f(-1)=2`.

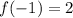Hence, the value that completes the table is 2.

So, option D is correct.

Answer 2

For this case we have the following exponential function:

`f(x) = ((1)/(2))^x`
Evaluating the function for x = -1 we have:

`f(x)=((1)/(2))^(-1)`
By power properties we can rewrite the function.
We have then:

`f(x)= (1)/(((1)/(2))^1)`

`f(x)= (1)/((1)/(2))`

`f(x) = 2`
Answer:
The value that completes the table when x = -1 is:

`f(x) = 2`
D. 2