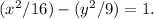Question

The equation of the hyperbola with foci (5, 0), (-5, 0) and vertices (4, 0), (-4, 0) is:

Answer 1

The equation of the hyperbola with given foci and vertices is
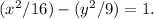`(x^2/16) - (y^2/9) = 1.` This is a horizontal hyperbola centered at the origin with a horizontal transverse axis.

Step-by-step explanation:

The equation of a hyperbola can be determined using the distance between its foci and vertices. For the hyperbola with foci at (5, 0) and (-5, 0), and vertices at (4, 0) and (-4, 0), the focal distance c is 5 and the distance a, which is the distance from the center to the vertices, is 4. To find the equation of the hyperbola, we also need to determine b, which is the distance from the center to the co-vertices, using the relationship
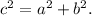`c^2 = a^2 + b^2.` Since the foci and vertices lie on the x-axis, this is a horizontal hyperbola, and the equation has the form
`(x^2/a^2) - (y^2/b^2) = 1.`

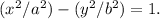
To find b, we calculate:
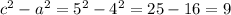`c^2 - a^2 = 5^2 - 4^2 = 25 - 16 = 9`, so b = √9 = 3. Therefore, the equation of the hyperbola is
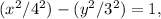`(x^2/4^2) - (y^2/3^2) = 1,`which simplifies to
`(x^2/16) - (y^2/9) = 1.`

Answer 2

y²/3²− x²/4²= 1 ,because two types of hyperbolas, one where a line drawn through its vertices and foci is horizontal, and one where a line drawn through its vertices and foci is vertical.