Question

The tens digit of a two-digit number is twice the units digit. If the digits are reversed, the new number is 36 less than the original number. Find the number.

Answer 1

Try this solution:
let the unknown two-digits number be 'xy'.
Then it is possible to write any two-digit number as 10x+y, where x - the tens digit and y - the unit digit.
Using the rule described above the phrase 'the tens digit of a number is twice the units digit' may be written as x=2y.
Using the same rule the phrase 'if the digits are reversed, the new number is 36 is less than the original number' may be written as (10x+y)-(10y+x)=36.
These two equations may be resolved as system of two equations:

`\left \{ {{x=2y} \atop {10x+y-(10y+x)=36}} \right. \ =\ \textgreater \ \ \left \{ {{x=8} \atop {y=4}} \right.`
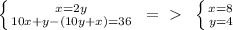
Check: the original number is 84, the new number is 48; difference is 84-48=36.

answer: 84