Question

Consider the following systems of linear inequalities.

x+2y>10
3x-4y>12
which of the following ordered pairs are solutions to the system

Answer 1

(7,2)

Explanation:

1. Firstly let's work with equalities respecting the conditions for these inequalities:

`\left\{\begin{matrix}x+2y>10 & \\ 3x-4y>12 & \end{matrix}\right.`

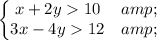
So let's pick two values for the first and the second equation greater than 10, and than 12.

Let's use the Addition Method, multiplying the

`\left\{\begin{matrix}x+2y=11 & \\ 3x-4y=13 & \end{matrix}\right.`

`\left\{\begin{matrix}x+2y=11 & *(2)\\3x-4y=13 & \end{matrix}\right.\\\left\{\begin{matrix}2x+4y=22 & \\ 3x-4y=13 & \end{matrix}\right.\\5x=35\\x=7\\\\x+2y=11\\(7)+2y=11\\2y=4\\y=2`

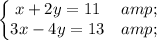
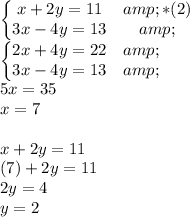
So, in this question there is not a list of options, but one of the possible pair is (7,2) the darker area below.