Question

Given : KLMN is a trapezoid

KF=1, MF || LK, altitude - h

Area of KLMF = Area of FMN

_____________________________________________

Find : KN

Answer 1

Proof:

KLMN- trapezoid Given
KF=1 Given
MF || LK Given
Altitude-h Given
A-KLMF=A-FMN Given
KF*h= FN*h/2 Area of Parallelogram
FN=2, KF=2 Area of Parallelogram
KN=KF+FN=3 Part-Whole Postulate

Answer 2

The measure of KN is 3 units.

Step-by-step explanation:

Given information: KLMN is a trapezoid , KF=1, MF || LK, altitude - h , Area of KLMF = Area of FMN

It means KLMF is a parallelogram with base KF=1 and height=h.

The area of a parallelogram is

`A=base* height`

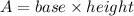
The area of KLMF is

`A_1=1* h=h`

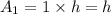
In triangle FMN, base FN and height h.

The area of a triangle is

`A=(1)/(2)* base* height`

`A_2=(1)/(2)* FN* h`

`A_2=(h)/(2)(FN)`

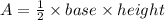
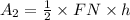
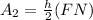
It is given that

Area of KLMF = Area of FMN

`h=(h)/(2)(FN)`

`2h=h(FN)`

`2=FN`

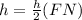
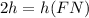
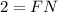
The length of FN is 2 units.

The length of KN is

`KN=KF+FN=1+2=3`

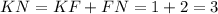
Therefore the measure of KN is 3 units.