as you know, the diagonals in a rhombus meet in the center at right-angles, check the picture below.
and the pair of angles at each opposite vertex, are twins.
now, since the diagonals center meeting point, makes 4 right-triangles, let's use the one on the upper-left, recall that a triangle has a sum of all interior angles to be 180°, so the missing angles in that triangle are "complementary angles", namely, they add up to 90°.
so, let's check 90 in a 4:5 ratio then, we simply divide 90 by (4+5) and distribute the pieces accordingly, let's do so,
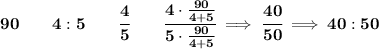
so the ratio of 4 angle, is really 40°, and the ratio of 5 angle is really 50°.
since the diagonal is bisecting the vertex, the angle made at the vertex is twice as much as that in the triangle we used, thus,
2(40) are the angles at the top and bottom, and
2(50) are the angles at the left and right.
80°, 80° and 100° and 100°.