Question

Solve 3log2^x=27.
the ans for this is 8 please help me slove this

Answer 1

So we have the equation
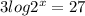
`3log2^(x)=27`, and we want to solve for
`x`.

First, we are going to apply the log of a power rule:
`loga^(x)=xloga`

`3log2^(x)=27`

`3xlog2=27`

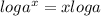
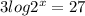
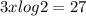
Next, we are going to divide both sides of the equation by
`3log2`:

`3xlog2=27`

`(3xlog2)/(3log2) = (27)/(3log2)`

`x= (27)/(3log2)`

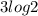
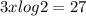
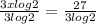
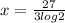
Last but not least, we can use a calculator to evaluate the right hand side of the equation:

`x= (27)/(3log2)`

`x=29.8974`

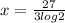
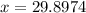
We can conclude that the solution of our logarithmic function is
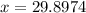
`x=29.8974`. I don't know who told you that the correct answer is 8, but they is wrong.