Question

Let f(x)=3x-6 and g(x)=x-2. Find the value of f/g and its domain

Answer 1

f(x)=3x-6
g(x)=x-2
(f/g)(x)=f(x)/g(x)=(3x-6)/(x-2)
(f/g)(x)=(3x-6)/(x-2)

x-2≠0
x-2+2≠0+2
x≠2

Domain of (f/g)(x)=R-{2}=(-Infinite,2) U (2, Infinite)
where R: all real numbers

If x≠2, then:
(f/g)(x)=(3x-6)/(x-2)
Getting common factor 3 in the numerator:
(f/g)(x)=3(3x/3-6/3)/(x-2)
(f/g)(x)=3(x-2)/(x-2)
(f/g)(x)=3

Answers:
The value of f/g=3
Domain of (f/g)(x)=R-{2}=(-Infinite,2) U (2, Infinite)
where R: all real numbers

Answer 2

f(x) = 3x - 6
g(x) = x - 2


`(f(x))/(g(x))= (3x-6)/(x-2) \\ \\ = (3(x-2))/(x-2) \\ \\ =3`

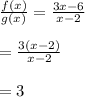
This means the value of the ratio f(x)/g(x) will be equal to 3.

Domain of the fraction is Set of All real numbers except 2. At 2 the given fraction will be undefined as the denominator in the very first fraction will be zero. Another reason 2 is not a part of the domain is that it will make x-2 equal to zero and we cannot cancel out 0 with 0 from numerator and denominator.

In interval notation, the domain will be: (-∞,2)∪(-2 ,∞)