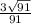Find the value of tangent for angle A

Question

asked Nov 10, 2019 131k views

2 Answers

Anil Maddala · Answer 1 · 2019-11-17T02:21:16+0000

Answer:

A)
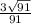
(3√(91) )/(91)

Explanation:

From the given right triangle, we need to find the missing side AC using the Pythagorean theorem.

The theorem said that the sum of the square of the sides is equal to the square of the hypotenuse.

Here hypotenuse AB = 40, one side BC = 12

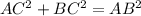
AC^2 + BC^2 = AB^2

Now plug in the given values and find the missing side AC.

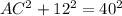
AC^2 + 12^2 = 40^2

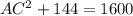
AC^2 + 144 = 1600

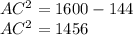
$AC^2 = 1600 - 144\\AC^2 = 1456$

Taking square root on both sides, we get

AC =4√91

Now we have to find the tanA.

Tan = Opposite/Adjacent

Here Opposite side = BC and Adjacent side AC of angle A.

Therefore,

tanA = BC/AC

tanA =
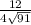
(12)/(4√(91) )

Since we have radical in the denominator, we need to multiply both the numerator and the denominator by √91, we get

tan A =
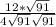
(12*√(91) )/(4√(91)√(91) )

tan A =
(3√(91) )/(91)