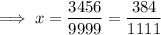Question

Convert 0.345634563456…to a rational number in the form of ab, where b≠0.

Answer 1

Since 0.345634563456… has four repeating digits, the numbers 3456 should be placed over a denominator containing four 9s.

0.345634563456…=

3456

9999

This fraction could also be written in simplest form as

3456

9999

=

384

1111

.

Explanation:

Answer 2

A standard trick for finding the rational form of a repeated decimal:


`x=0.34563456\ldots=0.\overline{3456}`

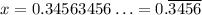
Multiply by an appropriate power of 10 to move one "cycle" of the repeated pattern to the left side of the decimal point:


`\implies10^4x=3456.34563456\ldots=3456.\overline{3456}`

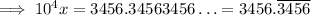
Now subtract
`x` from this number and we lose the fractional part:


`\implies10^4x-x=9999x=3456`

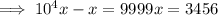
And from here you can solve for
`x`.


`\implies x=(3456)/(9999)=(384)/(1111)`