Answer:
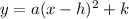
Where
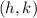 represents the coordinates of the vertex, the points where the parabola returns.
represents the coordinates of the vertex, the points where the parabola returns.
1.
In the first exercise (number 7 in the image), we observe that the vertex is at
 , and a points that is on the parabola could be
, and a points that is on the parabola could be
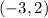 . So, with this information, we can find the
. So, with this information, we can find the
 parameter and form the parabola equation. Replacing all these, we have
parameter and form the parabola equation. Replacing all these, we have
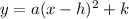

Then, we solve for


Now we have all the parameters, the equation of the first parabola is

2.
In the second exercies (number 8 in the image), the vertex or returning point is at
 , and one point on the parabola is (3,-3). Doing the same process as we did in the first exercise, we have
, and one point on the parabola is (3,-3). Doing the same process as we did in the first exercise, we have
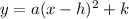
Replacing all values, that is,
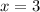 ,
,
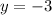 ,
,
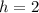 and
and
 .
.

So, the equation of this parabola is

3.
(Number 9 in the image). We apply the same process here. The vertex is at
 , one point on the parabola is
, one point on the parabola is
 . Then, we replace in the explicit form to find
. Then, we replace in the explicit form to find


Observe that the parameter
 is negative, that indicates the parabola is downside.
is negative, that indicates the parabola is downside.
So, the equation is

4.
(Number 10 in the image). Vertex at (-1,-1), one point on the parabola is (-2,-2). Replacing

So, the equation is

5.
(Number 11 in the image). Vertex at (1,2) and point at (2,4). Replacing

The equation would be

6.
(Number 12 in the image). Vertex at (3,-2), point at (2.0). Replacing in the explicit form, we have

So, the equation is

So, there you have all equations of each parabola. The process in the same for all of them.