Answer:
The variance of the data set is 1.28, approximately.
Explanation:
The variance is defined by
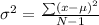
Where
 is the mean and
is the mean and
 is the total number of rings.
is the total number of rings.
First, we find the mean
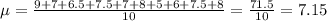
Then, we subtract the means with each element
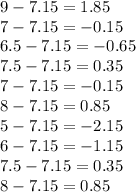
Now, we elevate each difference to the square power

Then, we sum all these results
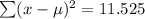
Now, we replace in the formula
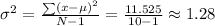
Therefore, the variance of the data set is 1.28, approximately.